Former Doctoral Candidate and EU early-stage researcher | Materials Science and Engineering
Current position: Postdoctoral Researcher at Ecole des Ponts ParisTech & Gustave Eiffel University
University of Limoges (France)
Advisors: Marc Huger
Itasca Mentor: Sacha Emam

Introduction
Predicting the mechanical behavior of heterogeneous materials, such as rocks, concretes, and ceramics, is complicated due to their complex microstructures, influencing the apparent behavior. In the case of industrial refractory ceramics, which could be damaged due to external mechanical loads or internal stresses (caused by thermal loading), an extensive microcrack network may appear that could significantly impact the apparent mechanical responses. In this case, due to a very high number of discontinuities, the Discrete Element Method (DEM) is an adequate alternative numerical method as it can simultaneously manage initiation and propagation of many cracks. Hence, the general aim of this study is to develop numerical models and techniques based on DEM to investigate the role played by the microstructure of such materials in macroscopic thermomechanical behavior.
Numerical Framework and Model
The principal numerical method for this study is DEM. The chosen DEM contact model is the Flat Joint Model (FJM), as FJM is able to mimic the microstructure of angular, interlocked grains, which are similar to rocks in the context of geomechanics. This concept of mimicking such interlocked granular materials is, in fact, very close to the general microstructure of refractory ceramics, which are constituted of large, interlocked aggregates within a finer matrix. FJM is implemented within the Particle Flow Code (PFC), which is the main numerical framework used in this study.
The report is divided into two parts:
- Implementation of periodic homogenization for two-phase materials in DEM (PFC3D) and its verification by experimental, analytical, and numerical approaches.
- Proposing a discrete-continuous hybrid approach to model the fracture behavior of refractory ceramics by using DEM/FJM simulations in order to reproduce key phenomena such as crack branching and diffused damage creation during the Wedge Splitting Test (WST) (optimization).
The first part is described below.
Modeling the Elastic Properties of Two-phase Materials Using Periodic Homogenization
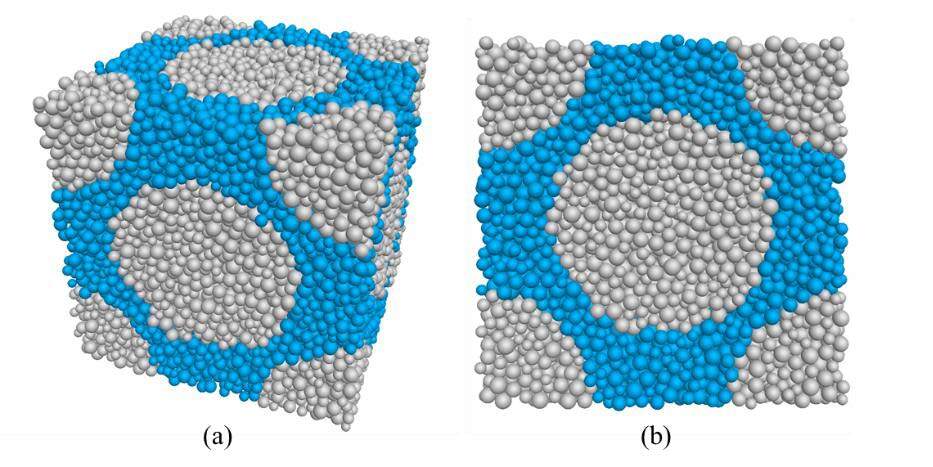
The main objective of this study was to simulate the elastic properties of two-phase materials by using periodic homogenization at the boundaries of 3D Representative Volume Elements (RVE) in order to work with a limited number of discrete elements to limit calculation time. The critical point was to accurately reproduce macroscopic elastic properties with a small number of inclusions (aggregates or voids) within a continuous matrix. The chosen RVE had a Faced Center Cubic (FCC) Arrangement in combination with Periodic Boundary Conditions (PBC), which allows accurate estimation of the macroscopic elastic properties of two-phase or porous materials.
Periodic Boundary Condition (PBC) and Creating Representative Volume Elements (RVE)
In order to reproduce a statistically isotropic behavior of two-phase materials, a microstructure with a low degree of anisotropy was necessary. Specifically, the Face-Centre Cubic (FCC) arrangement had shown a low degree of anisotropy for a periodic homogenization and was therefore chosen to represent the two-phase material (a matrix-inclusion system). As the matrix-inclusion system included two different constituents, it was necessary to assign different contact properties for the matrix and inclusion regions. Figure 1 shows the matrix in blue and the inclusions in grey. A total number of 20,000 discrete elements was sufficient for the RVE with regard to computation time and result accuracy. In fact, the periodic boundaries were used for the numerical models to remove any imposed boundary effects.
Reference Values from Previous Experimental Works Combined with Analytical and Numerical Models
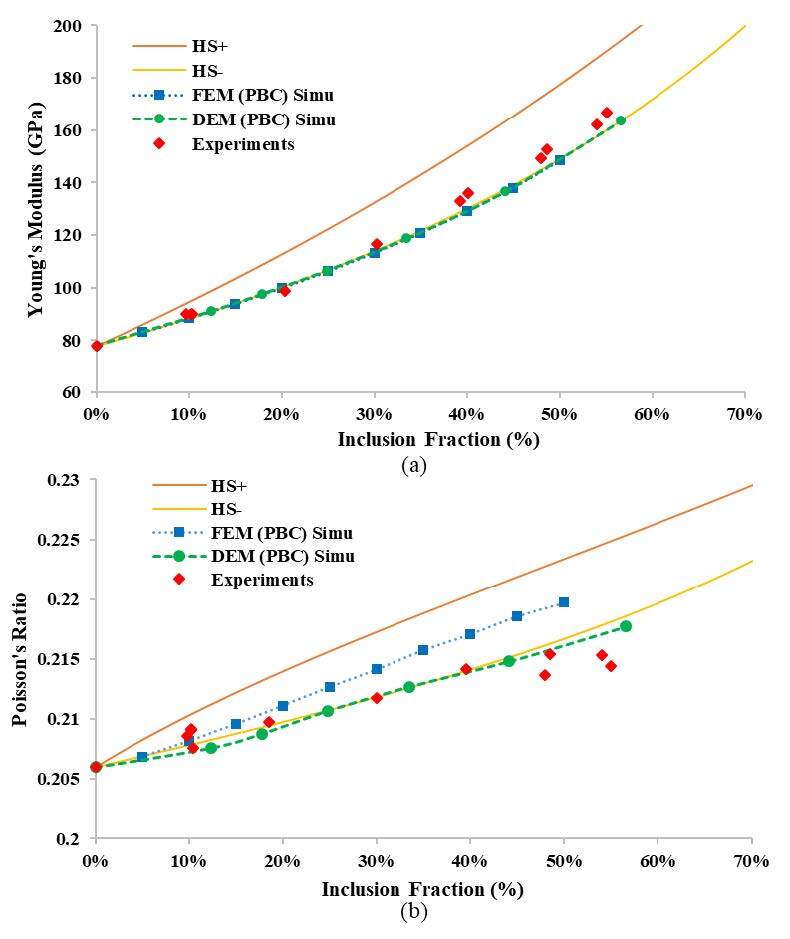
To verify the periodic homogenization in the DEM model for two-phase materials, it was essential to compare the obtained simulated results to experimental data and other predictive methods. First, a comparison was made to experimental results on the two-phase model material. Second, the results were compared to other existing methods for the prediction of elastic properties of two-phase materials: namely, an analytical method by Hashin and Shtrikman relationships and a numerical approach using the Finite Element Method (FEM) simulations.
Results
As seen in Figure 2, the obtained results for different inclusion volume fractions were successfully compared to macroscopic elastic properties of experimental composites and theoretical, analytical bounds of Hashin & Shtrikman (HS) and FEM simulations. The results validated the DEM numerical approach using a homogenization technique (PBC combined with a small RVE), which can be used to optimize the microstructure when designing materials such as concretes or ceramics. In this way, by working with a reasonable number of discrete elements, the proposed numerical approach reduces calculation time while giving valid results.
References
Hashin Z., Shtrikman S. (1963) A Variational Approach to the Theory of the Elastic Behaviour of Multiphase Materials, Journal of the Mechanics and Physics of Solids, Volume 11, Issue 2, Pages 127-140,
ISSN 0022-5096, https://doi.org/10.1016/0022-5096(63)90060-7.